INTRODUCCIÓN

El dibujo es una forma de comunicación de permite expresar de modo sencillo ideas que resultarían muy complicadas de explicar sólo con palabras. Recordar el dicho: ” una imagen vale más que mil palabras ”.Imaginar si tuviéramos que expresar sólo con palabras la descripción de un edificio, de un avión, o de cualquier objeto tecnológico. Tendríamos que escribir un libro completo para simplemente describir la información gráfica contenida en unos pocos planos, resultando muchísimo más difícil y lento de interpretar. De un cuadro cualquiera que tengamos en nuestra casa podríamos decir lo mismo, sería imposible poder describir con palabras la imagen reflejada, y la sensación que recibiría una persona que leyera la descripción sería completamente distinta a la recibida al visualizar el cuadro.

El dibujo técnico surge como un medio de expresión y comunicación indispensable, tanto para el desarrollo de procesos de investigación sobre las formas y diseños, como para la comprensión gráfica de bocetos y proyectos tecnológicos, cuyo último fin es la creación de productos que pueden tener un valor utilitario y la comprensión e interpretación de aplicaciones técnico-prácticas.

Para todo esto es necesario el conocimiento de un conjunto de convencionalismos que están recogidos en las normas para el dibujo técnico, que se establecen en un ámbito nacional e internacional.

Su finalidad última es adquirir una visión general del dibujo técnico más sencillo y utilizado a la vez que ayuda a formalizar o visualizar lo que se está diseñando o creando y contribuye a proporcionar, desde una primera concreción de posibles soluciones, hasta la última fase del desarrollo donde se presentan los resultados en dibujos definitivamente acabados.

GEOMETRÍA

La palabra Geometría procede de dos palabras griegas que son: geo que significa tierra y metron que significa medida. La unión de ambas palabras – geometría – significa medida de la tierra.

Hace más de 2000 años los egipcios que vivían en las orillas del río Nilo y se dedicaban a la agricultura, tenían problemas con las crecidas que este río provocaba. Cuando las aguas del Nilo inundaban las tierras y al retirarse dejaban sustancias que enriquecían los campos para futuras cosechas, producía también un problema, y es que borraba las señales de los límites de los campos.
Cada agricultor tenía señalada en el suelo las medidas de sus terrenos. Cuando las aguas se retiraban y borraban las señales, se volvían a medir las tierras. Los encargados de hacer las nuevas mediciones eran los agrimensores.
La palabra agrimensor significa: encargado de medir la tierra.

¿DE QUÉ SE OCUPA LA GEOMETRÍA?

Como ni estamos en Egipto ni nos dedicamos, por ahora, a la agricultura, es lógico que hoy, la Geometría se ocupe del estudio de algo más que de medir terrenos. La Geometría que es una rama de las Matemáticas estudia: los puntos geométricos, rectas, planos, curvas, polígonos, poliedros, superficies, volúmenes, etc.
Comenzamos el estudio de la Geometría por el:

PUNTO GEOMÉTRICO

¿Qué es un punto geométrico?
El punto es la parte, el elemento, la cosa más simple y una de las más importantes de la Geometría.
Un punto no tiene medidas, es decir, no puedes medir su anchura o largura. Solo apreciamos el lugar donde se encuentra.
Imagina que tienes un papel sobre la mesa y dejas caer el bolígrafo de punta. Al impactar contra el papel deja una pequeña señal y cuando nos referimos a ella, hablamos de punto.

Es costumbre representarlo por una cruz y a un lado la letra por la que le identificamos
Ejemplos:

El lugar donde se cortan o se juntan las rectas es el punto (en color rojo que para lograr verlo hemos de ampliar la imagen) y las hemos representado con las letras A y B. Las denominamos: punto A y  punto B.
Cuando hablamos de intersección de dos o más líneas nos referimos a las líneas que se cortan. La palabra intersección procede de dos palabras latinas: inter que significa entre y sectio que significa corte.

RECTA

La recta es un conjunto de puntos colocados unos detrás de otros en la misma dirección.
La línea recta no tiene principio ni fin. Cuando dibujamos una línea recta, en realidad, representamos una parte de ella. Unas veces la representamos con dos letras mayúsculas que se refieren a dos de sus puntos, o bien, con una letra minúscula:

Toma un trozo de  hilo por los extremos, cada uno con una mano y ténsalo fuerte. De este modo obtienes una recta.
La recta es la distancia más corta entre dos puntos.

SEMI-RECTA

Cuando en una recta señalas un punto, a cada uno de los tramos a ambos lados de la misma llamamos semi-recta:

Como puedes observar, la recta que pasa por el punto A ha quedado dividida en dos partes representadas por las semirrectas m y n.
Podemos decir que una semi-recta es parte de una recta que tiene principio u origen y no tiene fin.
 Las semirrectas m y n, tienen origen en A.

A la primera semirrecta la podemos representar:

A la segunda semirrecta la representamos:

Las dos semirrectas de una misma recta siempre son opuestas y además tienen el mismo origen. Las puntas de flecha nos indican que tienen sentidos OPUESTOS o CONTRARIOS, la semirrecta m tiene sentido hacia la izquierda y la semirrecta n tiene sentido hacia la derecha.

15.1  Si en una recta señalas un punto ¿en cuántas partes queda dividida la recta? ¿cómo se llaman cada una de las partes?

Respuesta: a) En dos partes b) semi-rectas.

15.2  En el ejercicio anterior ¿tienen algún punto en común las semirrectas?

Respuesta: Sí, el punto que hemos fijado.

15.3   ¿El punto común de dos semi-rectas es principio de una y final de otra?

Respuesta: No. Es principio de ambas.

SEGMENTO

Si sobre una recta señalas dos puntos, el trozo de esa recta llamamos segmento
En la figura siguiente tienes la recta r sobre la que hemos señalado dos puntos A y B. Al trozo de recta entre A y B llamamos segmento.

Cuando veas la notación  se refiere al segmento existente entre A y B. Casi siempre, a los segmentos los designamos con letras mayúsculas.

15.4   Si en una recta fijas dos puntos ¿en cuántas partes has dividido a la recta?

Respuesta: En tres partes.

15.5  ¿Cuántas semirrectas y cuántos segmentos creamos al fijar dos puntos en una recta?

Respuesta: 2 semirrectas y un segmento.

Solución:
En la figura que tienes a continuación puedes ver:

1) Los puntos A y B.
2) Las semirrectas  m y n
3) El segmento AB

Las semirrectas m y n  tienen principio u origen pero no tienen fin.
La porción de recta (en color rojo) comprendida entre los puntos A y B es un segmento.

15.6  Si decimos que una semirrecta tiene un origen, el final ¿dónde se encuentra?

Respuesta: En el infinito, no tiene límite. 
15.7  Dos semirrectas ¿pueden tener un punto común?

Respuesta: Sí, el punto origen de ambas.

15.8   ¿Cuántos puntos necesito para trazar una recta que los incluya?

Respuesta: Dos puntos.

15.9  ¿Existe alguna diferencia entre recta y semirrecta?

Respuesta: Sí, la recta no tiene ni principio ni fin, la semirrecta aunque tampoco tiene fin, sí tiene un origen.

15.10   Si unimos dos semirrectas opuestas ¿qué resultado obtenemos?
Respuesta: La recta.

EL PLANO

Si en este momento estás leyendo lo que está escrito en esta página, es que miras a la pantalla del ordenador. Te habrás fijado que la pantalla es una superficie lisa, llana, plana,…lo mismo que la tapa de tu pupitre, el cristal de tu ventana, etc.
Todos estos ejemplos representan el plano.

El plano tiene dos dimensiones: largo y ancho:

En el plano podemos dibujar puntos, líneas, etc.
                                   
Debes tener presente:
a) Entre dos puntos sólo existe una recta.

b) Por un punto pueden pasar infinitas rectas:

Por el punto P pasan cuantas rectas desees.

A tener en cuenta:
a) Si sobre un plano o superficie plana dibujas una recta, todos sus puntos están contenidos en dicho plano o superficie plana.
b) Un plano puede contener infinitas rectas.

c) Por una recta pueden pasar infinitos planos:

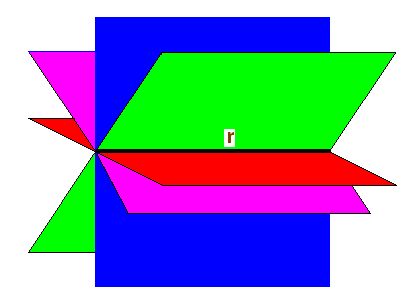
Por la recta r  (en color negro) pueden pasar infinitos planos.

TRES PUNTOS NO SITUADOS EN LÍNEA RECTA DETERMINAN UN PLANO:

Casi siempre que nos referimos a un plano o superficie plana nos imaginamos 4 esquinas o vértices. La realidad es un poco distinta, para definir o determinar un plano nos es suficiente con tres puntos que no estén en la misma recta:

Los puntos A, B y C no están en la misma recta, aunque 2 de ellos sí lo están. Siempre que los tres puntos no se encuentren en la misma recta, al unirlos, crearemos un plano, y solamente uno:

Si la figura te parece como parte de un plano no importa, siempre será un plano.

 

 

SEMIPLANO

Una recta trazada en un plano, le divide a éste en dos semiplanos, lógicamente las partes no es necesario que sean iguales:

La recta r ha creado dos semiplanos.

A cada zona en la que ha sido dividido el plano se le puede llamar región, porción de plano, banda, además de semiplano.
A la recta que divide a un  plano en dos regiones o semiplanos se la conoce también con el nombre de frontera o recta frontera.

15.12  Una recta y un punto fuera de ella ¿pueden definir un plano? ¿Por qué?
Respuesta: Sí. Porque dos puntos de la recta y un tercer punto no contenido en ella, determinan 1 plano (tres puntos no situados en línea recta determinan un plano).

15.13   Un punto situado en un plano ¿ocupará siempre alguna de las dos regiones o semiplanos?

Respuesta: No, el punto puede estar situado en la recta que divide al plano.

15.14   Dos puntos situados en dos semiplanos ¿qué determinan?
Dibuja.

Respuesta: Un segmento (tiene principio y fin).

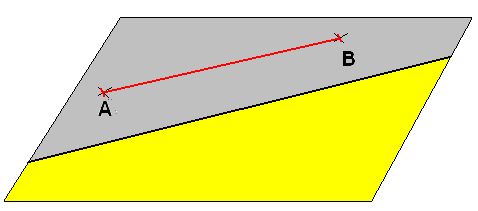
15.15  ¿Puedes asegurar que cualquier segmento que une dos puntos situados en distintas regiones de un plano cortarán a la recta frontera o la recta de división?

Respuesta: Sí.

15.16  Si dos puntos estuviesen en el mismo semiplano, el segmento que los une ¿puede llegar a cortar a la recta de frontera?
Comprueba dibujando.

Respuesta: No.

Dibujo:

LÍNEAS PARALELAS

Las líneas que situadas en el mismo plano no se tocan por mucho que las prolonguemos son líneas paralelas:

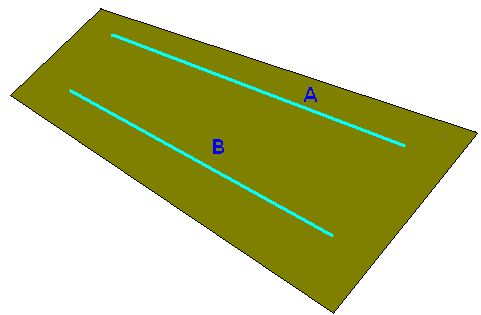
Las rectas A y B son paralelas. Las vías del tren son paralelas. En todos los puntos, las distancias entre ambas líneas es siempre la misma.

15.17  Si tienes una recta y un punto no perteneciente a esta recta ¿cuántas rectas paralelas a la recta anterior pueden pasar por dicho punto? Contesta después de haberlo comprobado con un dibujo.

Respuesta: Solamente una recta que sea paralela a la dada.